Fitting synthetic data including covariates
fitting_synthetic_data_including_covariates.Rmd
library(epidp)
library(ggplot2)
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
library(magrittr)
library(purrr)
#>
#> Attaching package: 'purrr'
#> The following object is masked from 'package:magrittr':
#>
#> set_names
library(tidyr)
#>
#> Attaching package: 'tidyr'
#> The following object is masked from 'package:magrittr':
#>
#> extract
options(mc.cores = 4)In this document, we explore how the incorporation of covariate information affects estimation of .
Added Gaussian noise around a sinusoidal covariate-driven mean
# define sinusoidal Rt with noise
rt_fun <- function(t, x) {
x[1] * exp(x[2])
}
nt <- 200
t <- 1:nt
f <- 1.3 + 1.2 * sin(4 * (pi / 180) * t)
g <- vector(length = nt)
g[1] <- rnorm(1, 0, 1)
rho <- 0.8
for (i in 2:length(g)) {
g[i] <- rho * g[i - 1] + rnorm(1, 0, 0.1)
}
X <- matrix(c(f, g), nrow = length(f), ncol = 2)
# simulation parameters
mean_si <- 6.5
sd_si <- 4.03
i_0 <- 10
# data frame of outputs
epidemic_df <- simulate_renewal_epidemic(rt_fun, nt, mean_si, sd_si, i_0, X)
# plot
epidemic_df %>%
mutate(f = f) %>%
select(-c(w_dist, lambda_t)) %>%
pivot_longer(c(R_t, f)) %>%
ggplot(aes(x = t, y = value, colour = name)) +
geom_line() +
scale_y_continuous(
name = "Incidence (i_t)",
sec.axis = sec_axis(~ . / 1000, name = "Reproduction Number (R_t)")
) +
labs(x = "Time", colour = "Variable") +
theme_minimal()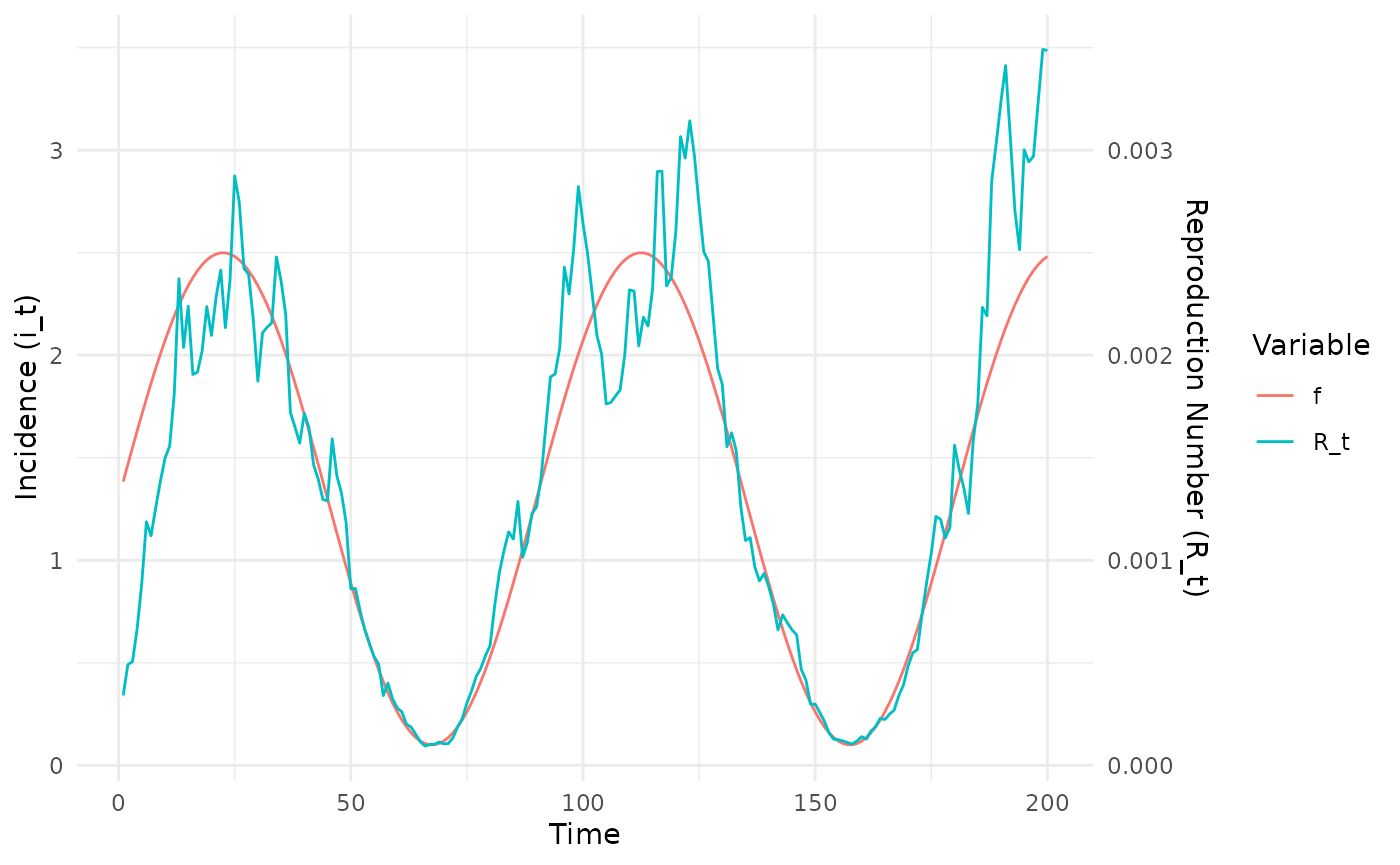 We first try to estimate
without covariate information. We now use a Stan version of EpiFilter to
estimate the
profile.
We first try to estimate
without covariate information. We now use a Stan version of EpiFilter to
estimate the
profile.
# fit model
fit <- fit_epifilter(
N = length(epidemic_df$i_t),
C = epidemic_df$i_t,
w = epidemic_df$w_dist,
iter = 200,
chains = 1 # to pass CRAN
)
#>
#> SAMPLING FOR MODEL 'epifilter' NOW (CHAIN 1).
#> Chain 1:
#> Chain 1: Gradient evaluation took 0.004281 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 42.81 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1:
#> Chain 1:
#> Chain 1: WARNING: There aren't enough warmup iterations to fit the
#> Chain 1: three stages of adaptation as currently configured.
#> Chain 1: Reducing each adaptation stage to 15%/75%/10% of
#> Chain 1: the given number of warmup iterations:
#> Chain 1: init_buffer = 15
#> Chain 1: adapt_window = 75
#> Chain 1: term_buffer = 10
#> Chain 1:
#> Chain 1: Iteration: 1 / 200 [ 0%] (Warmup)
#> Chain 1: Iteration: 20 / 200 [ 10%] (Warmup)
#> Chain 1: Iteration: 40 / 200 [ 20%] (Warmup)
#> Chain 1: Iteration: 60 / 200 [ 30%] (Warmup)
#> Chain 1: Iteration: 80 / 200 [ 40%] (Warmup)
#> Chain 1: Iteration: 100 / 200 [ 50%] (Warmup)
#> Chain 1: Iteration: 101 / 200 [ 50%] (Sampling)
#> Chain 1: Iteration: 120 / 200 [ 60%] (Sampling)
#> Chain 1: Iteration: 140 / 200 [ 70%] (Sampling)
#> Chain 1: Iteration: 160 / 200 [ 80%] (Sampling)
#> Chain 1: Iteration: 180 / 200 [ 90%] (Sampling)
#> Chain 1: Iteration: 200 / 200 [100%] (Sampling)
#> Chain 1:
#> Chain 1: Elapsed Time: 14.703 seconds (Warm-up)
#> Chain 1: 13.381 seconds (Sampling)
#> Chain 1: 28.084 seconds (Total)
#> Chain 1:
#> Warning in validityMethod(object): The following variables have undefined
#> values: log_likelihood[1]. Many subsequent functions will not work correctly.
#> Warning: The largest R-hat is NA, indicating chains have not mixed.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#r-hat
#> Warning: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#bulk-ess
#> Warning: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#tail-ess
# look at MCMC summaries
print(fit, c("sigma", "R"))
#> Inference for Stan model: epifilter.
#> 1 chains, each with iter=200; warmup=100; thin=1;
#> post-warmup draws per chain=100, total post-warmup draws=100.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
#> sigma 0.18 0.00 0.02 0.15 0.17 0.18 0.19 0.22 18 1.02
#> R[1] 1.09 0.06 0.43 0.44 0.77 1.05 1.35 1.99 56 1.00
#> R[2] 1.11 0.04 0.40 0.48 0.81 1.08 1.34 1.94 88 1.00
#> R[3] 1.11 0.04 0.36 0.51 0.85 1.06 1.36 1.90 83 0.99
#> R[4] 1.07 0.04 0.34 0.54 0.81 1.06 1.27 1.96 85 1.00
#> R[5] 1.04 0.03 0.29 0.62 0.81 1.04 1.22 1.75 77 1.03
#> R[6] 1.06 0.03 0.29 0.62 0.83 1.02 1.26 1.71 69 1.03
#> R[7] 1.06 0.03 0.28 0.62 0.87 1.03 1.25 1.62 83 1.04
#> R[8] 1.07 0.03 0.28 0.56 0.89 1.05 1.27 1.62 91 1.05
#> R[9] 1.10 0.03 0.27 0.62 0.89 1.11 1.28 1.64 74 1.03
#> R[10] 1.16 0.03 0.28 0.72 0.94 1.11 1.37 1.67 62 1.02
#> R[11] 1.26 0.03 0.29 0.77 1.06 1.20 1.45 1.91 93 0.99
#> R[12] 1.36 0.03 0.30 0.75 1.14 1.38 1.59 1.87 83 0.99
#> R[13] 1.49 0.03 0.33 1.00 1.23 1.50 1.69 2.16 101 1.01
#> R[14] 1.50 0.04 0.34 0.98 1.25 1.47 1.71 2.23 69 1.01
#> R[15] 1.53 0.04 0.35 0.93 1.28 1.50 1.79 2.22 66 1.00
#> R[16] 1.58 0.03 0.37 0.94 1.34 1.58 1.78 2.44 121 0.99
#> R[17] 1.62 0.03 0.34 1.01 1.40 1.65 1.80 2.37 104 1.00
#> R[18] 1.74 0.03 0.37 1.06 1.51 1.66 1.99 2.47 182 0.99
#> R[19] 1.82 0.03 0.38 1.19 1.56 1.76 2.04 2.66 160 0.99
#> R[20] 2.03 0.03 0.37 1.32 1.79 2.04 2.28 2.74 189 1.00
#> R[21] 2.07 0.04 0.38 1.35 1.81 2.09 2.33 2.79 120 1.00
#> R[22] 2.01 0.03 0.38 1.28 1.78 1.99 2.25 2.73 128 1.00
#> R[23] 1.98 0.03 0.31 1.43 1.77 1.96 2.15 2.70 153 0.99
#> R[24] 2.04 0.03 0.32 1.53 1.83 1.96 2.19 2.78 150 1.00
#> R[25] 2.18 0.03 0.36 1.68 1.91 2.13 2.40 3.01 163 0.99
#> R[26] 2.18 0.03 0.36 1.60 1.88 2.19 2.42 2.84 139 1.00
#> R[27] 2.06 0.03 0.33 1.47 1.80 2.04 2.32 2.68 138 1.00
#> R[28] 2.05 0.03 0.31 1.40 1.86 2.03 2.26 2.59 150 0.99
#> R[29] 1.98 0.02 0.30 1.48 1.76 1.96 2.17 2.59 200 0.99
#> R[30] 1.98 0.03 0.29 1.39 1.79 1.96 2.18 2.54 124 0.99
#> R[31] 1.96 0.03 0.25 1.55 1.78 1.96 2.07 2.52 81 1.02
#> R[32] 2.02 0.02 0.24 1.56 1.83 2.04 2.16 2.54 121 1.00
#> R[33] 2.00 0.03 0.24 1.63 1.84 1.95 2.16 2.54 90 1.01
#> R[34] 1.97 0.02 0.23 1.62 1.81 1.95 2.11 2.45 91 0.99
#> R[35] 1.97 0.02 0.24 1.60 1.81 1.93 2.12 2.47 103 0.99
#> R[36] 1.78 0.02 0.23 1.45 1.61 1.79 1.91 2.37 137 0.99
#> R[37] 1.72 0.02 0.20 1.42 1.55 1.69 1.84 2.10 94 0.99
#> R[38] 1.57 0.01 0.17 1.28 1.44 1.57 1.69 1.90 184 0.99
#> R[39] 1.58 0.02 0.17 1.30 1.48 1.57 1.69 1.94 116 0.99
#> R[40] 1.46 0.01 0.16 1.12 1.36 1.46 1.56 1.74 112 0.99
#> R[41] 1.45 0.01 0.16 1.13 1.37 1.47 1.56 1.74 133 0.99
#> R[42] 1.39 0.01 0.15 1.12 1.28 1.38 1.50 1.67 117 0.99
#> R[43] 1.21 0.01 0.15 0.95 1.11 1.21 1.31 1.49 117 0.99
#> R[44] 1.22 0.01 0.15 0.95 1.11 1.20 1.30 1.52 181 0.99
#> R[45] 1.19 0.01 0.11 1.01 1.11 1.18 1.25 1.43 117 0.99
#> R[46] 1.25 0.01 0.14 1.00 1.13 1.24 1.34 1.54 149 1.00
#> R[47] 1.23 0.01 0.14 0.98 1.14 1.23 1.32 1.50 101 1.00
#> R[48] 1.37 0.02 0.16 1.10 1.26 1.37 1.46 1.75 70 0.99
#> R[49] 1.33 0.02 0.15 1.10 1.23 1.31 1.43 1.62 77 0.99
#> R[50] 1.08 0.01 0.12 0.89 0.99 1.07 1.16 1.34 112 0.99
#> R[51] 0.92 0.01 0.12 0.66 0.85 0.92 1.00 1.13 129 0.99
#> R[52] 0.79 0.01 0.11 0.61 0.72 0.80 0.84 1.04 82 0.99
#> R[53] 0.69 0.01 0.10 0.52 0.62 0.68 0.75 0.86 92 0.99
#> R[54] 0.59 0.01 0.09 0.45 0.54 0.58 0.64 0.76 139 0.99
#> R[55] 0.53 0.01 0.08 0.38 0.47 0.52 0.58 0.70 82 1.06
#> R[56] 0.58 0.01 0.09 0.39 0.53 0.58 0.63 0.77 200 0.99
#> R[57] 0.45 0.01 0.07 0.31 0.41 0.46 0.50 0.59 110 0.99
#> R[58] 0.36 0.01 0.08 0.23 0.30 0.35 0.42 0.52 99 0.99
#> R[59] 0.32 0.01 0.08 0.19 0.25 0.31 0.37 0.47 187 0.99
#> R[60] 0.34 0.01 0.08 0.18 0.29 0.33 0.39 0.52 199 0.99
#> R[61] 0.28 0.01 0.07 0.17 0.23 0.28 0.32 0.44 127 1.01
#> R[62] 0.20 0.01 0.06 0.11 0.16 0.20 0.24 0.34 119 0.99
#> R[63] 0.15 0.01 0.05 0.07 0.11 0.14 0.18 0.27 97 1.00
#> R[64] 0.13 0.01 0.06 0.05 0.10 0.12 0.17 0.25 103 1.00
#> R[65] 0.11 0.01 0.06 0.04 0.06 0.10 0.14 0.23 17 1.14
#> R[66] 0.09 0.01 0.06 0.02 0.05 0.08 0.12 0.22 30 1.09
#> R[67] 0.09 0.01 0.05 0.02 0.06 0.09 0.12 0.21 59 1.00
#> R[68] 0.12 0.01 0.06 0.03 0.07 0.12 0.15 0.26 67 1.01
#> R[69] 0.16 0.01 0.08 0.04 0.11 0.15 0.21 0.32 76 1.01
#> R[70] 0.17 0.02 0.10 0.04 0.10 0.16 0.22 0.39 36 1.01
#> R[71] 0.17 0.02 0.10 0.03 0.10 0.14 0.22 0.45 35 0.99
#> R[72] 0.19 0.02 0.12 0.02 0.10 0.17 0.27 0.48 31 0.99
#> R[73] 0.24 0.02 0.12 0.09 0.15 0.23 0.30 0.54 30 0.99
#> R[74] 0.26 0.02 0.13 0.06 0.16 0.24 0.31 0.57 29 0.99
#> R[75] 0.29 0.02 0.13 0.09 0.18 0.29 0.38 0.56 30 1.00
#> R[76] 0.32 0.02 0.14 0.14 0.22 0.29 0.40 0.65 39 0.99
#> R[77] 0.36 0.02 0.15 0.14 0.24 0.35 0.43 0.67 56 1.00
#> R[78] 0.42 0.03 0.20 0.15 0.28 0.40 0.50 0.87 58 1.00
#> R[79] 0.48 0.03 0.23 0.19 0.31 0.43 0.60 0.98 64 1.01
#> R[80] 0.53 0.04 0.26 0.18 0.34 0.48 0.67 1.05 45 1.05
#> R[81] 0.56 0.04 0.27 0.20 0.36 0.51 0.73 1.10 39 1.09
#> R[82] 0.64 0.05 0.31 0.22 0.44 0.58 0.81 1.29 40 1.14
#> R[83] 0.70 0.06 0.34 0.25 0.45 0.63 0.88 1.53 33 1.17
#> R[84] 0.78 0.07 0.36 0.33 0.51 0.68 0.99 1.65 27 1.22
#> R[85] 0.81 0.08 0.38 0.31 0.53 0.75 1.02 1.70 24 1.25
#> R[86] 0.87 0.08 0.41 0.25 0.51 0.83 1.12 1.79 24 1.20
#> R[87] 0.94 0.08 0.46 0.33 0.58 0.85 1.22 2.10 30 1.14
#> R[88] 1.01 0.09 0.48 0.33 0.66 0.90 1.29 2.25 29 1.12
#> R[89] 1.09 0.09 0.47 0.34 0.73 1.04 1.37 2.15 28 1.11
#> R[90] 1.16 0.08 0.46 0.42 0.80 1.14 1.45 2.09 30 1.12
#> R[91] 1.28 0.09 0.47 0.41 0.95 1.25 1.59 2.27 25 1.12
#> R[92] 1.39 0.10 0.49 0.48 1.03 1.30 1.72 2.45 27 1.15
#> R[93] 1.48 0.08 0.48 0.62 1.14 1.41 1.81 2.54 33 1.11
#> R[94] 1.63 0.09 0.55 0.70 1.18 1.59 1.94 2.82 41 1.07
#> R[95] 1.77 0.08 0.52 0.91 1.38 1.75 2.04 2.93 46 1.07
#> R[96] 1.85 0.09 0.55 0.89 1.45 1.82 2.20 2.99 35 1.11
#> R[97] 1.93 0.09 0.54 1.05 1.52 1.90 2.22 2.95 34 1.10
#> R[98] 2.01 0.08 0.54 1.19 1.59 1.93 2.40 3.16 49 1.04
#> R[99] 2.12 0.08 0.56 1.22 1.76 2.02 2.49 3.34 51 1.05
#> R[100] 2.20 0.07 0.56 1.31 1.83 2.12 2.46 3.55 60 1.05
#> R[101] 2.28 0.07 0.55 1.42 1.87 2.20 2.68 3.42 62 1.05
#> R[102] 2.38 0.07 0.54 1.53 1.98 2.35 2.67 3.71 56 1.02
#> R[103] 2.42 0.06 0.50 1.58 2.07 2.42 2.77 3.66 70 1.02
#> R[104] 2.52 0.06 0.49 1.67 2.17 2.50 2.82 3.67 65 1.01
#> R[105] 2.48 0.05 0.46 1.65 2.15 2.46 2.75 3.55 81 0.99
#> R[106] 2.49 0.05 0.46 1.68 2.16 2.44 2.78 3.44 83 0.99
#> R[107] 2.45 0.04 0.44 1.73 2.14 2.40 2.70 3.33 115 1.01
#> R[108] 2.45 0.04 0.38 1.71 2.23 2.46 2.64 3.31 77 1.02
#> R[109] 2.41 0.04 0.37 1.85 2.14 2.34 2.64 3.23 71 1.01
#> R[110] 2.42 0.03 0.32 1.86 2.22 2.41 2.63 3.06 94 1.00
#> R[111] 2.44 0.03 0.32 1.75 2.26 2.47 2.62 2.99 110 0.99
#> R[112] 2.47 0.03 0.38 1.68 2.24 2.47 2.72 3.15 155 0.99
#> R[113] 2.51 0.03 0.35 1.96 2.26 2.48 2.75 3.27 127 1.00
#> R[114] 2.55 0.03 0.32 2.04 2.32 2.52 2.76 3.20 124 0.99
#> R[115] 2.73 0.03 0.37 2.06 2.46 2.70 2.96 3.45 115 0.99
#> R[116] 2.77 0.04 0.39 2.08 2.46 2.77 3.02 3.60 114 1.01
#> R[117] 2.75 0.03 0.39 2.15 2.42 2.72 3.05 3.40 148 0.99
#> R[118] 2.73 0.03 0.35 2.12 2.43 2.75 2.98 3.40 99 0.99
#> R[119] 2.69 0.03 0.32 2.10 2.45 2.71 2.90 3.33 111 0.99
#> R[120] 2.68 0.03 0.32 2.11 2.43 2.71 2.86 3.28 90 1.02
#> R[121] 2.85 0.03 0.27 2.37 2.63 2.82 3.04 3.40 101 0.99
#> R[122] 2.75 0.03 0.26 2.19 2.55 2.75 2.93 3.21 109 0.99
#> R[123] 2.54 0.02 0.23 2.18 2.35 2.54 2.67 3.03 111 1.00
#> R[124] 2.56 0.03 0.25 2.13 2.39 2.54 2.69 3.07 79 0.99
#> R[125] 2.44 0.02 0.19 2.12 2.31 2.44 2.60 2.81 98 0.99
#> R[126] 2.43 0.02 0.23 2.03 2.26 2.41 2.61 2.85 113 1.01
#> R[127] 2.45 0.02 0.20 2.09 2.33 2.42 2.60 2.78 120 1.00
#> R[128] 2.24 0.02 0.17 1.89 2.12 2.24 2.36 2.54 75 1.00
#> R[129] 1.94 0.02 0.18 1.56 1.83 1.95 2.06 2.31 90 1.00
#> R[130] 1.93 0.02 0.19 1.60 1.79 1.91 2.06 2.30 68 1.00
#> R[131] 1.80 0.02 0.15 1.53 1.72 1.79 1.88 2.10 72 1.01
#> R[132] 1.62 0.02 0.14 1.39 1.53 1.61 1.70 1.88 52 1.03
#> R[133] 1.54 0.01 0.11 1.31 1.47 1.54 1.61 1.75 129 1.01
#> R[134] 1.35 0.01 0.12 1.16 1.28 1.35 1.43 1.57 94 0.99
#> R[135] 1.12 0.01 0.10 0.93 1.04 1.11 1.19 1.33 106 0.99
#> R[136] 1.05 0.01 0.09 0.90 0.99 1.04 1.11 1.26 137 0.99
#> R[137] 1.00 0.01 0.08 0.84 0.95 0.99 1.05 1.16 159 1.00
#> R[138] 0.83 0.01 0.08 0.65 0.77 0.82 0.89 0.98 89 0.99
#> R[139] 0.79 0.01 0.07 0.67 0.75 0.79 0.82 0.92 87 0.99
#> R[140] 0.86 0.01 0.08 0.70 0.80 0.85 0.92 1.02 94 1.00
#> R[141] 0.81 0.01 0.07 0.69 0.76 0.80 0.85 0.93 133 0.99
#> R[142] 0.73 0.01 0.08 0.59 0.67 0.73 0.79 0.86 90 1.03
#> R[143] 0.73 0.01 0.07 0.62 0.68 0.73 0.78 0.86 116 0.99
#> R[144] 0.71 0.01 0.08 0.56 0.65 0.70 0.75 0.87 74 1.03
#> R[145] 0.67 0.01 0.08 0.56 0.62 0.67 0.73 0.84 48 1.03
#> R[146] 0.64 0.01 0.07 0.52 0.59 0.63 0.67 0.77 102 0.99
#> R[147] 0.48 0.01 0.05 0.37 0.45 0.48 0.51 0.58 97 0.99
#> R[148] 0.38 0.01 0.06 0.26 0.35 0.38 0.41 0.48 104 1.00
#> R[149] 0.27 0.01 0.05 0.17 0.24 0.27 0.30 0.37 96 1.01
#> R[150] 0.29 0.00 0.05 0.20 0.26 0.29 0.33 0.40 142 0.99
#> R[151] 0.29 0.00 0.06 0.20 0.25 0.28 0.33 0.41 142 0.99
#> R[152] 0.23 0.01 0.05 0.14 0.19 0.23 0.26 0.32 82 0.99
#> R[153] 0.17 0.00 0.04 0.10 0.14 0.17 0.20 0.25 123 0.99
#> R[154] 0.19 0.00 0.05 0.11 0.16 0.18 0.20 0.33 117 0.99
#> R[155] 0.13 0.00 0.05 0.05 0.09 0.12 0.16 0.24 176 1.01
#> R[156] 0.11 0.00 0.05 0.04 0.08 0.10 0.13 0.23 142 1.00
#> R[157] 0.14 0.00 0.05 0.05 0.10 0.14 0.16 0.23 105 1.01
#> R[158] 0.14 0.01 0.05 0.06 0.10 0.13 0.16 0.24 107 1.07
#> R[159] 0.15 0.01 0.06 0.04 0.11 0.13 0.18 0.26 84 1.03
#> R[160] 0.17 0.01 0.06 0.08 0.13 0.17 0.22 0.30 113 1.04
#> R[161] 0.16 0.01 0.07 0.05 0.12 0.16 0.21 0.31 77 0.99
#> R[162] 0.19 0.01 0.07 0.07 0.13 0.18 0.24 0.33 60 1.02
#> R[163] 0.23 0.01 0.09 0.09 0.16 0.23 0.29 0.42 79 0.99
#> R[164] 0.34 0.01 0.11 0.14 0.24 0.34 0.41 0.59 78 1.01
#> R[165] 0.42 0.01 0.13 0.22 0.33 0.42 0.49 0.71 80 0.99
#> R[166] 0.48 0.02 0.16 0.22 0.37 0.47 0.57 0.81 80 0.99
#> R[167] 0.52 0.02 0.17 0.26 0.39 0.48 0.63 0.84 113 0.99
#> R[168] 0.55 0.03 0.20 0.23 0.41 0.52 0.64 0.97 56 1.00
#> R[169] 0.64 0.02 0.21 0.30 0.49 0.62 0.79 1.09 92 1.01
#> R[170] 0.73 0.02 0.22 0.34 0.59 0.71 0.87 1.18 83 1.00
#> R[171] 0.84 0.03 0.26 0.34 0.67 0.78 1.05 1.32 81 0.99
#> R[172] 0.92 0.04 0.28 0.49 0.68 0.90 1.12 1.51 61 0.99
#> R[173] 1.01 0.03 0.26 0.54 0.85 1.03 1.16 1.52 72 1.00
#> R[174] 1.05 0.04 0.30 0.52 0.86 1.06 1.23 1.67 69 0.99
#> R[175] 1.13 0.04 0.33 0.59 0.88 1.13 1.36 1.85 67 0.99
#> R[176] 1.21 0.04 0.33 0.67 0.96 1.18 1.44 1.88 74 0.99
#> R[177] 1.27 0.03 0.32 0.75 1.08 1.26 1.45 2.02 90 0.99
#> R[178] 1.26 0.03 0.33 0.76 1.05 1.22 1.46 2.06 95 1.00
#> R[179] 1.33 0.04 0.34 0.70 1.13 1.31 1.50 2.05 93 1.01
#> R[180] 1.42 0.04 0.36 0.89 1.13 1.38 1.66 2.13 97 1.01
#> R[181] 1.51 0.04 0.37 0.96 1.24 1.48 1.72 2.36 108 1.03
#> R[182] 1.62 0.03 0.36 1.05 1.37 1.60 1.83 2.40 114 1.01
#> R[183] 1.78 0.03 0.40 1.14 1.49 1.70 2.01 2.67 160 1.02
#> R[184] 2.03 0.03 0.37 1.38 1.79 1.99 2.26 3.00 123 1.02
#> R[185] 2.20 0.03 0.34 1.53 2.01 2.19 2.40 2.95 111 1.05
#> R[186] 2.32 0.03 0.38 1.67 2.09 2.29 2.55 3.12 179 1.03
#> R[187] 2.54 0.03 0.37 1.94 2.29 2.49 2.76 3.24 181 0.99
#> R[188] 2.74 0.03 0.33 2.17 2.51 2.70 2.96 3.50 157 0.99
#> R[189] 2.82 0.04 0.35 2.28 2.53 2.79 3.09 3.55 89 1.00
#> R[190] 2.83 0.04 0.40 2.13 2.53 2.78 3.19 3.51 99 0.99
#> R[191] 2.84 0.04 0.37 2.17 2.53 2.80 3.14 3.49 109 0.99
#> R[192] 2.90 0.03 0.32 2.34 2.68 2.84 3.15 3.49 106 0.99
#> R[193] 2.93 0.02 0.31 2.38 2.71 2.93 3.16 3.50 167 0.99
#> R[194] 2.90 0.02 0.29 2.21 2.72 2.95 3.06 3.44 153 0.99
#> R[195] 3.05 0.04 0.29 2.47 2.87 3.04 3.25 3.71 68 1.00
#> R[196] 3.11 0.02 0.25 2.61 2.98 3.10 3.28 3.63 106 1.00
#> R[197] 3.00 0.03 0.27 2.56 2.82 2.98 3.19 3.50 112 1.00
#> R[198] 3.23 0.02 0.27 2.69 3.05 3.23 3.47 3.64 153 1.01
#> R[199] 3.57 0.03 0.29 2.97 3.35 3.57 3.79 4.09 103 0.99
#> R[200] 3.81 0.04 0.31 3.21 3.59 3.85 4.03 4.37 79 0.99
#>
#> Samples were drawn using NUTS(diag_e) at Thu Nov 14 19:49:45 2024.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
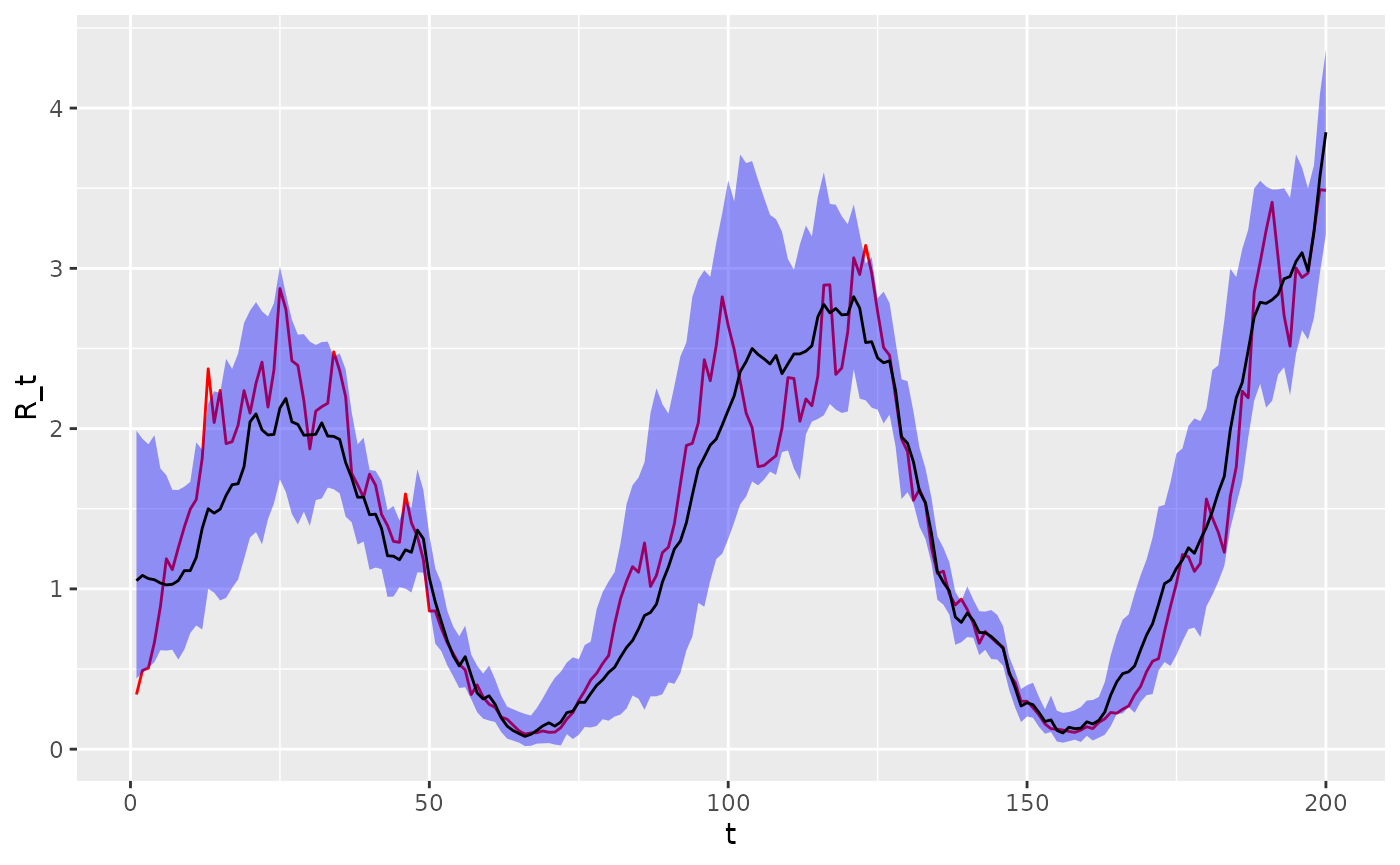
#> convergence, Rhat=1).We now overlay the estimated versus the actual values. The estimated values coincide reasonably with the true values.
# extract posterior quantiles
R_draws <- rstan::extract(fit, "R")[[1]]
lower <- apply(R_draws, 2, function(x) quantile(x, 0.025))
middle <- apply(R_draws, 2, function(x) quantile(x, 0.5))
upper <- apply(R_draws, 2, function(x) quantile(x, 0.975))
# plot
epidemic_df %>%
mutate(
lower = lower,
middle = middle,
upper = upper
) %>%
select(t, R_t, lower, middle, upper) %>%
ggplot(aes(x = t, y = R_t)) +
geom_line(colour = "red") +
geom_ribbon(aes(ymin = lower, ymax = upper), fill = "blue", alpha = 0.4) +
geom_line(aes(y = middle))